Chapter 9 - Finding Front Doors

9.1 Looking Ahead

Copy link

The prospect of identifying the answer to your research question by closing all back doors is actually kind of daunting. Think about everything you have to do. You have to model the data generating process, you have to list out all the paths, you have to find a set of variables that close all the back doors, and you have to measure and control for all of those variables.

Tough work! Especially that last part. Actually controlling for everything is surprisingly tricky, especially in social science where there are so many things that might matter that you’re almost certain to run into a variable you have to control for but can’t. Even if it’s possible to measure, it’s probably not in your data. “Attitude towards risk,” “Curiosity,” “Customer sentiment,” “Intellectual ability” - these are all things that you might well find sitting on a bad path but don’t have access to in your data.

Even worse, because there are so many variables that might be on back doors, what are the odds you’re actually going to think of them all and include them in your causal diagram? Seems pretty likely that you’d miss one.130130 For this reason, you don’t have to look hard to find researchers who would distrust any causal claim made using an approach of closing bad doors by controlling for things. Much of economics is this way. Those researchers would instead focus on the kinds of designs described in this chapter, and detailed much more fully in the second half of this book.

Sounds bad. So what to do? An alternate approach to identifying the answer to a research question is to, instead of actively closing back doors, find ways of isolating just Front Doors. If we can estimate the Front Doors directly, we don’t need to worry about closing back doors.

How is this possible? This can work in two different ways: either find a setting in which only some of the variation in Treatment has back doors, but some of the variation has no back doors, or at least only has back doors you can close - natural experiments - or you can estimate individual arrows on the Front Door paths even if the overall effect isn’t identified - the front door method.

For example, imagine trying to estimate the effect of Wealth on Lifespan. There are bound to be plenty of back door paths on that causal diagram, passing through all kinds of variables you don’t have data on, like “Business Skill,” “Willingness to Commit Robberies,” and so on.

But how about wealth among people who play the lottery? Certainly, for most of the variation in wealth between people who play the lottery, they got it through means like working, inheritance, or buying assets, and for that variation in wealth all those same back doors are there. However, among people who buy lottery tickets, work, inheritance, and buying assets have nothing to do with whether you win the lottery. So if your research design focuses just on differences in wealth driven by lottery winnings among people who play the lottery - surprise! No back doors on that variation.131131 Of course, you might also think that the effect of lottery wealth might be different from the effect of wealth overall. And you’d be correct - this analysis would give you only the effect of lottery wealth, not wealth overall, which might be your actual interest. Technically this analysis would give you a “local average treatment effect,” which we’ll discuss further in Chapter 10.

9.2 Trying to Push a String

Copy link

So how can we pick out just the variation we want? It all comes down to the fact that your treatment variable varies for different reasons. If A, B, and C are all causes of treatment, then A, B, and C are all reasons why treatment varies from one person to another. If you’re lucky, some of those reasons lead to variation that has back doors, and other reasons don’t. If you’re even luckier, you can actually isolate just the part that doesn’t have back doors.

The key idea here is that we can partition the variation in Treatment. By either selecting a particular sample or using certain approaches to statistical adjustment, we can throw out the part that is driven by all that nasty back door business, and leave ourselves to do analysis with just another part that isn’t. Then we focus on the part that isn’t so we don’t have to worry about back doors.

Perhaps the cleanest application of this approach is the randomized controlled experiment. In a randomized controlled experiment, the researcher actually steps in and assigns treatment (or the absence of treatment) to people, and watches the resulting differences in outcome.

You’re probably familiar with the concept. You probably did a few in your science classes in middle school. You may even be familiar with the idea that randomized experiments are sometimes referred to as the “gold standard” of causal research designs.132132 Is that actually true? Randomized experiments have their pros and cons compared to research using observational data. The identification is, obviously, much easier and more believable with a randomized experiment. On the other hand, people might not behave as they normally would when they’re part of an experiment. Or the logistical limitations of recruiting participants may mean that experimental samples aren’t great representations of the wider population. Plus, samples tend to be smaller in experiments. There are no easy answers. But why do they work?

Experiments work because they create a form of variation in the treatment that has no back doors. If the treatment was assigned randomly, then for everyone in the experiment, variation in all the variables on all the back doors should be unrelated to whether they got the treatment or not. So all the back doors are closed!

Let’s say we’re interested in figuring out whether charter schools improve students’ test scores more (or less) than traditional public schools, a hot-button issue in the United States and a frequent setting for isolating front doors (⊕Chabrier, Cohodes, and Oreopoulos 2016Chabrier, Julia, Sarah Cohodes, and Philip Oreopoulos. 2016. “What Can We Learn from Charter School Lotteries?” Journal of Economic Perspectives 30 (3): 57–84.). There are a whole lot of variables that cause you to attend a charter school or not, with race, background, personality, location, and academic interest giving us only a few. No way we could control for enough things to close all those back doors. This is represented by the unobservable AllKindsaStuff in Figure 9.1.

Figure 9.1: The Effect of Charter Schools on Student Achievement

However, our diagram doesn’t stop there. A lot of charter schools have more interested students than they have slots, and many of them assign those slots by lottery, providing a convenient setting for lots of experimental analyses. So the diagram really looks like Figure 9.2.

Figure 9.2: The Effect of Charter Schools on Student Achievement with a Lottery

Notice a few things: First, there are no back doors from Lottery to StudentAchievement. The effect of LotteryWin on StudentAchievement is identified in the data without any controls. Second, the only way that Lottery can affect StudentAchievement is through Charter. So if we calculate the effect of LotteryWin on StudentAchievement, that must really be telling us about the effect of Charter on StudentAchievement.

This all works because there are now two reasons why people go to Charters. The first is because of AllKindsaStuff - that part’s fraught, let’s avoid it. The second is because of the LotteryWin. If we can isolate just the part driven by Lottery, we’ve identified the answer to our research question.

We can analyze the data from this experiment in a few ways:

1. Throw out all the data where Charter isn’t driven by Lottery, and then look at the effect of Charter on StudentAchievement. In this context that means throwing out data from any schools without a lottery, or data from any students that got in through means other than the lottery, or any students who weren’t even eligible for the lottery. Just take the students who were in the lottery and compare the ones who got into the Charter against the ones who didn’t.133133 This is what most people think of when they think of experiments - you only use the data from the experiment.
2. Use LotteryWin to explain or predict Charter. Then, take your prediction of whether someone goes to a Charter, which is based purely on their LotteryWin. Because this prediction is based only on LotteryWin and not AllKindsaStuff, the variation in the prediction contains none of the back doors of AllKindsaStuff. So then look at the relationship between the prediction and StudentAchievement to get the effect.134134 This is the instrumental variable method, which will be covered more thoroughly in Chapter 19. Some other methods in the second part of this book apply variations on this idea.

In both approaches we isolate just the variation in Charter driven by LotteryWin and throw out the rest of the variation, either by tossing out data subject to the rest of the variation, or by focusing just on the variation we estimate to be due to LotteryWin.

This makes clear two things - first, that a randomized experiment very cleanly lets us identify the causal effect we’re interested in, and second, that a randomized experiment requires us to focus on a very narrow slice of the data: the slice that is randomized. If that data doesn’t represent the wider population, we won’t get to our true effect no matter how big the sample is, or how clean the identification. This is one suspicion that some researchers have about charter school lotteries - that the schools that hold lotteries, and the students that enter them, aren’t representative of the broader populations of charter schools and students, respectively, and so don’t quite answer the question we want.135135 To account for all of this, we’d have to add some nodes onto our diagram like ChoosesToEnterLottery.

Putting that to the side, we definitely get a very clean identification. But to do this we need explicit randomization. This whole book is premised on the idea that this isn’t always possible or feasible! So what else can we do?

9.3 What the World Can Do for Us

Copy link

A “natural experiment” is a real-world setting in which some sort of randomization has been done for us. In fact, you may have noticed a little cheat in the last section - that charter school study isn’t a randomized controlled trial. It just so happens that the charter schools did some randomization. It wasn’t researchers assigning things.136136 At least not in most charter schools. That already is an example of a natural experiment - the randomization occurred in the world; the researcher just came along to take advantage of it. The “wealth of lottery winners” example from earlier works like this too. Researchers don’t decide who wins the lottery. But among lottery winners, there’s randomization in who gets the big prize.

So the randomization doesn’t need to be researcher-controlled. But can we go further? Does it even need to be as random as an explicit lottery? What does “randomization” mean, anyway?

We can think about natural experiments by considering what makes randomized experiments work in the first place. They work because they fix some of the variation in treatment to have no back doors. As long as we can make that magic happen, we have a working natural experiment.

So what we need to think about is whether we can find a source of variation in treatment that has no open back doors. We can call this a “source of exogenous variation.”Any path we can walk from the source of exogenous variation to the outcome must be (a) closed, or (b) contain our treatment.137137 This is clearly true of actual randomization - there’s no way for the randomization to affect the outcome except by causing you to be treated. So it’s exogenous (not caused by anything else in the data generating process) and any link between the randomization and our outcome must be because of the treatment itself. An ideal source of exogenous variation is not caused by any other variable that belongs on the causal diagram.

This means that we can use plenty of things as sources of exogenous variation even if they’re not purely random, as long as they’re as good as random in the context of our data generating process.

What does the causal diagram for this look like? It looks… almost exactly like a randomized controlled trial! You can see for yourself in Figure 9.3.

Figure 9.3: A Basic Natural Experiment Diagram

There are four real differences between randomized controlled experiments and natural experiments.

1. Sometimes there will be back doors from the NaturalRandomness to the Outcome, which doesn’t happen with pure randomization. For example, let’s say we’re using the fact that Sesame Street became available at different times in different areas to examine the effects of kids watching Sesame Street. That’s not purely random - it likely became available earlier in larger markets like urban areas, so there’s a back door with SesameStreetTiming \(\leftarrow\) Urban \(\rightarrow\) Outcome. But as long as we can control for something to shut the back door down, we’re okay. The process is the same as when we’re identifying the effect of our treatment by controlling for things - the idea here is that we’re just picking a variable where the back doors are easier to control for.
2. Natural experiments are, well, more natural. People may not even realize they’re a part of an experiment (in fact, nobody, including the researcher, may notice there’s an experiment happening at all until long after it’s over). So the observations you get may be more realistic. Sample sizes tend to be bigger, too. And people usually don’t have to volunteer to be part of the experiment, so your sample isn’t made up of a bunch of volunteer-types.
3. Because, just like in an experiment, we are isolating just the variation in treatment that is driven by the NaturalRandomness, we are tossing out any treatment that occurs for other reasons. So we are seeing the effect only among people who are sensitive to NaturalRandomness - if the effect would be different among another group of people, we won’t see it for them. Some parents would never let their kids watch Sesame Street no matter whether it’s available or not. Maybe Sesame Street would be even better for those kids than for the kids who do see it. But we’ll never learn with a natural experiment!138138 This issue will be discussed further in Chapter 10.
4. People believe the exogeneity of pure randomization. But convincing people that your not-perfectly-random source of exogenous variation is exogenous in your data generating process, given that we’re doing social science where everything is related to everything else, can be a tall order. Is there really only one back door from SesameStreetTiming to Outcome?

That last difference is a big one, and for some people it puts them off all but the purest and cleanest natural experiments. Does this whole process even work at all? Let’s take a look at some example studies and see how far they can get.

9.4 Is it Too Good to be True?

Copy link

For our first study, let’s expand on what we already know: lotteries. Scott Hankins, Mark Hoekstra, and Paige Skiba published a study in 2011 on the effect of winning the lottery on declaring bankruptcy later (⊕Hankins, Hoekstra, and Skiba 2011Hankins, Scott, Mark Hoekstra, and Paige Marta Skiba. 2011. “The Ticket to Easy Street? The Financial Consequences of Winning the Lottery.” Review of Economics and Statistics 93 (3): 961–69.). Specifically, they looked at the Florida lottery, and only included people who had won some amount of money in the lottery.

They look only at people who had won some amount of money, rather than at everybody, to remove any variation based on the kind of people who play the lottery in the first place. If everyone in your sample plays the lottery, you’ve controlled for variables related to being the kind of person who plays the lottery.

Within that group, winning a really big prize should be completely random. They then compare people who win really big prizes (between $50,000 and $150,000) against people who won smaller prizes (less than $10,000). They find that winning a big prize reduces your chances of declaring bankruptcy initially, but after a while it doesn’t seem to matter - the prize just pushed bankruptcy to a later date, rather than reducing the chances you go bankrupt. You can see their results in Figure 9.4. People who win small prizes (the dashed line) have basically the same bankruptcy rates whether it’s before the prize or after, which makes sense. For people who win big prizes (the solid line), in the few years immediately following the prize, bankruptcies fall. However, by three years after the prize they spike back up, and then revert to matching those who won a small prize. In the aggregate, the effect on bankruptcy seems to be just pushing it from 1-2 years in the future to 3 years in the future.

## Error in detach("package:tm") : invalid 'name' argument

## Error in detach("package:NLP") : invalid 'name' argument

Figure 9.4: Winning the Lottery and Going Bankrupt, from Hankins, Hoekstra, and Skiba (2011)

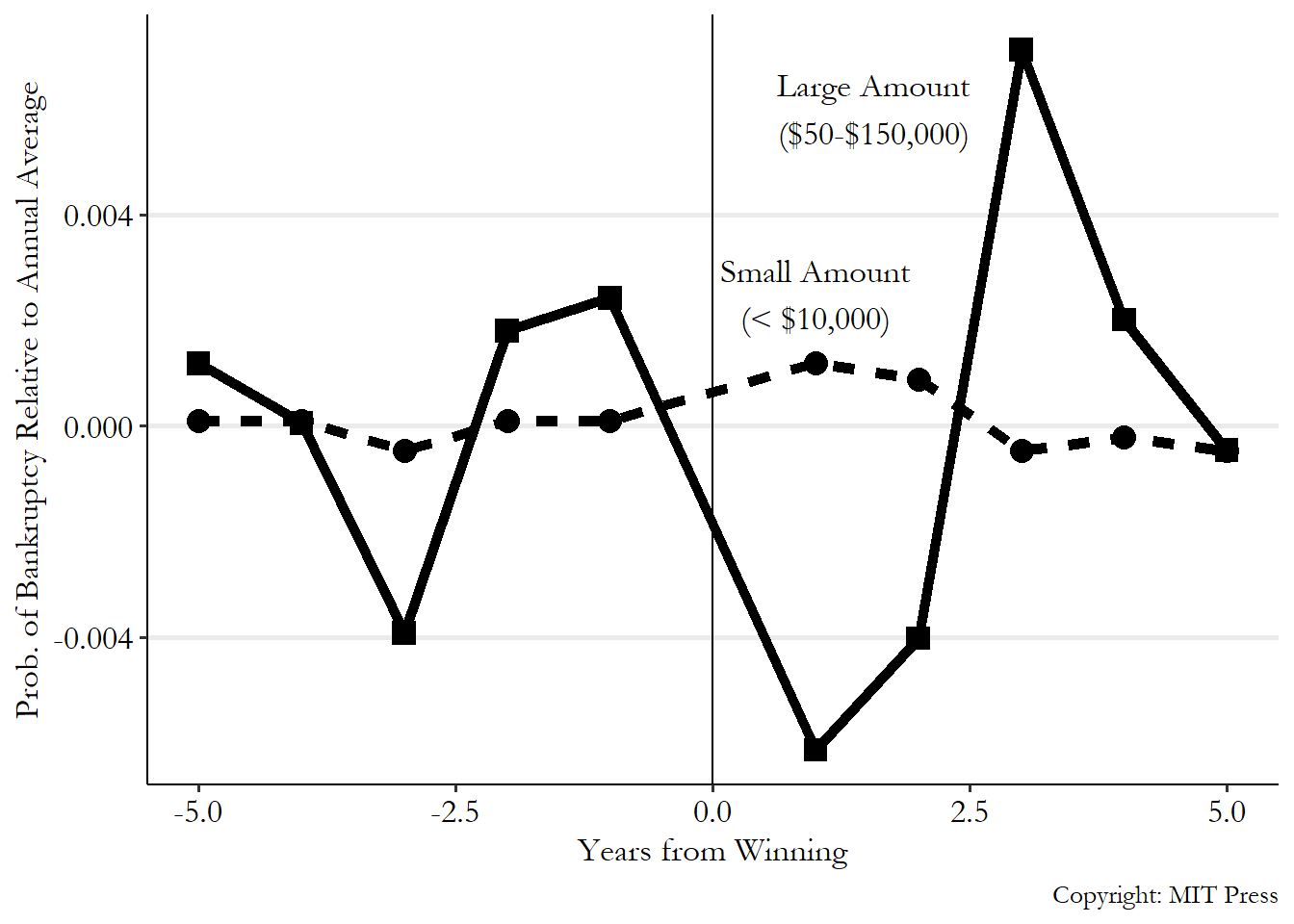
What needs to be true for this to work? It really needs to be the case that winning is random. So they do a number of things to make sure that’s true. They check whether the chances of winning seem to be related to anything they observe, such as the characteristics of where the winner lives. Nope! No relationship, which is a relief. However, there is one thing they come up with - the rules of the Florida lottery changed over time, altering the number of small-prize winners. If bankruptcies also change over time, we have a Winner \(\leftarrow\) Time \(\rightarrow\) Bankruptcy back door. So they control for the year in which the prize was given to account for this.

These results seem pretty solid!139139 At least in design. We might be slightly concerned that the big-prize winners in Figure 9.4 have bankruptcy rates that seem to jump up and down before they win, too. This might be an issue of noise introduced by not having that many big-prize winners. It’s hard to imagine another reason why winning the lottery would be related to being bankrupt other than… because you won the lottery. Of course, these results only apply to the kind of people who play the lottery, but at least for that group in Florida, winning a big lottery prize doesn’t seem to reduce your chances of going bankrupt in the long run.

So when the world provides us with actual literal randomization, that gives us a convincing design. Let’s go further and use a study where the source of exogenous variation is less clearly random: the wind. Pan He and Cheng Xu (⊕Xu 2019Xu, Cheng. 2019. “Essays on Urban and Environmental Economics.” PhD thesis, The George Washington University.) look at whether air pollution being worse causes people to drive more. The research question makes sense - if it’s smoggy and unpleasant outside, you’re not going to want to walk, bike, or maybe even take the bus. But that’s a problem. Cars cause pollution. So if pollution causes cars… well, that spiral isn’t going anywhere good.

He and Xu get their data from Beijing, where pollution is quite bad. They look at whether people drive more on days when there is more pollution, and find that they do. However, pollution is related to all sorts of things that may also be related to driving, like whether the factories are running. Back doors are afoot! They find an exogenous source of pollution variation in the direction of the wind. In Beijing, a west-blowing wind blows pollution into the city. By isolating just the variation in pollution driven by wind direction, they find that an increase in daily pollution large enough to change the government’s rating from “not polluted” to “polluted” increases driving by 3%.

Is the direction of the wind exogenous? It certainly seems unlikely that anything relevant to car-driving or pollution caused the wind.140140 I’m actually not at all sure what causes the wind to blow in certain directions. Probably ask a meteorologist on that one. However, it may well be that there are still back doors. For example, the direction of the wind might change with the season, and the season is certainly related to pollution and driving. The weather is likely to be related to all of these things, too. The causal diagram might look like Figure 9.5

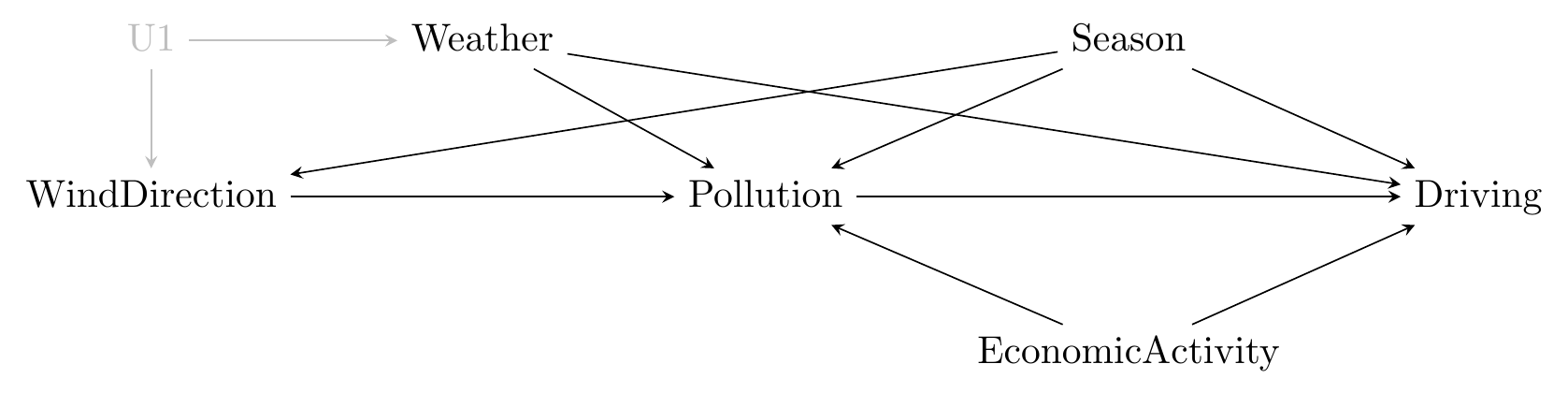
Figure 9.5: The Effect of Pollution on Driving in Beijing

So as long as we can control for season and weather - and they do - then they should be good to go. Of course, that’s the thing! Are we certain that we’ve properly laid out all of the back doors? Are we missing anything? If we miss anything important, this won’t work.

I find the use of wind direction here pretty compelling evidence. But it’s certainly not as rock solid as the lottery. Remember, the difficulties of identifying the effect of \(X\) on \(Y\) by controlling to close back doors are the same here. We’re just hoping to pick a variable that’s easier to close back doors for than \(X\).

How far from true randomization can we go? As far as our assumptions are willing to take us - and as far as we’re willing to carry those assumptions along.

Let’s take a look at Camilleri and Diebold (⊕2019Camilleri, Susan, and Jeffrey Diebold. 2019. “Hospital Uncompensated Care and Patient Experience: An Instrumental Variable Approach.” Health Services Research 54 (3): 603–12.), who look at the effect of uncompensated care - medical care given by hospitals that they don’t end up being paid for - on patient experience. You can imagine that if hospitals are spending a bunch of money giving care that they don’t get paid for, they’re going to have fewer resources available to give patients the best experience.141141 This takes place in the United States medical system where patients are expected to pay for care, and if they can’t the hospital is sometimes on the hook for it.

The amount of uncompensated care a hospital gives is related to all sorts of back-door stuff. The kinds of patients they get and how likely those patients are to pay, the kinds of procedures they’re known for, and so on. Camilleri and Diebold need a source of exogenous variation. They use the 2014 Medicaid expansion, in which some states but not others expanded access to the Medicaid program. Medicaid expansion considerably increased health insurance coverage in the states that accepted the additional aid. That additional coverage meant that there would be more compensation available for hospitals. Using this source of exogenous variation, they find that reductions in uncompensated care did improve patient experience, but only by a little bit.

Does this work as a source of exogenous variation? We can definitely imagine some back doors. After all, states didn’t accept or reject Medicaid at random; the choice was highly politicized. States with different kinds of governments were more or less likely to expand Medicaid. The authors controlled for state and local characteristics to close these back doors.

Of course, the policy changed plenty of things about health care other than just improving hospital compensation. Medicaid expansion, and thus expanded access to insurance, should change lots of things about health care besides hospital compensation that might also be related to patient experience. We have to be willing to assume that the expansion really only affected hospital compensation in order to think of the variation in compensation driven by the Medicaid expansion as being exogenous.142142 Note that we’re describing front doors from the Medicaid expansion here. If we wanted to know the effect of the Medicaid expansion itself, we’d want these included. But since we want to use Medicaid expansion to isolate just the part of uncompensated care that has no back doors, these are still bad paths that will mess up our research design.

So does this study work? Sure! As long as the assumptions we’ve just laid out about Medicaid expansion only working through hospital compensation sound reasonable. If we aren’t willing to swallow those assumptions, then no, it doesn’t work.143143 This is true for all studies, since all studies rely on assumptions. It’s not that some studies have assumptions and others don’t. Rather, we might just find one study’s assumptions more believable than another’s, given what we know about the real world. There are lots of studies that use policy implementation as a source of exogenous variation like this. It’s certainly a viable path, but we need to be very careful in thinking what assumptions we have to make about the data generating process, and whether those assumptions are true.

Isolating front paths is always feasible, just like identifying the effect of a treatment by closing back doors is always feasible, even if we don’t have anything even remotely like purely-random variation as we would in a randomized experiment or even a lottery. However, the farther away we get from that pure randomization, the more things we need to control for, and the more assumptions we have to make, and perhaps the more unbelievable assumptions we have to make. This isn’t a magic formula; we’re just replacing the difficulty of finding and closing all back doors for a treatment variable with the difficulty of finding and closing all back doors for something else.

9.5 Riding a Shooting Star

Copy link

Ah, but there is another way in which we can identify the causal effect of a treatment on an outcome by isolating front doors. It is called, appropriately, the “front door method,” and it works very differently from the concepts covered so far in this chapter. It also sees a lot less usage in the real world and serves only as a tiny little coda to this chapter.

The reason the approach with the seems-pretty-important name of “front door method” gets tucked away in the last section of a chapter all about isolating front doors is that it only applies in very specialized scenarios. For a long time, applied researchers didn’t really even think about it as a possible research design. And now that they do know about it in theory, they’re scratching their heads thinking about when they could ever really use it in practice. So we’ll talk about it here, briefly, and heck, maybe you can think about how it might be useful.

The front door method works when your causal diagram looks something like Figure 9.6, when there’s a bad path that can’t be closed, such as if W in that diagram can’t be measured.

Figure 9.6: A Diagram the Front Door Method Works On

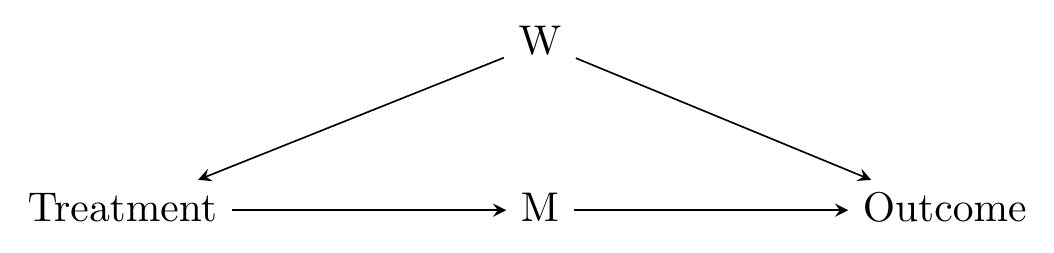
In Figure 9.6, if W can’t be measured, then we can’t control for anything to identify the effect of Treatment on Outcome.

However, maybe we can identify something else. How about the effect of Treatment on M? We can identify that - the only back door is Treatment \(\leftarrow\) W \(\rightarrow\) Outcome \(\leftarrow\) M. But Outcome is a collider on that path so it’s already closed. We don’t need to worry about it.

What else can we identify? How about the effect of M on Outcome? The only back door is M \(\leftarrow\) Treatment \(\leftarrow\) W \(\rightarrow\) Outcome, and we can control for Treatment to close that back door path.

So we can identify both Treatment \(\rightarrow\) M and M \(\rightarrow\) Outcome. We just need to combine those two effects to get our effect Treatment \(\rightarrow\) M \(\rightarrow\) Outcome.

We can use the classic example given when discussing the front door method: smoking (⊕Pearl and Mackenzie 2018Pearl, Judea, and Dana Mackenzie. 2018. The Book of Why: The New Science of Cause and Effect. New York City, New York: Basic Books.). It’s difficult to figure out the effect of smoking on something like cancer rates because there are lots of things related to whether you smoke (background, income, health-mindedness, etc.) that can be hard to measure and would also be related to cancer rates. So we have a lot of back doors we can’t close.

But what if we have something that sits between smoking and cancer - some measurable reason why smoking causes cancer? Let’s say that thing is TarInLungs. In this simplified fantasy, the only reason Smoking causes Cancer is because it causes TarInLungs, and TarInLungs causes Cancer.144144 Although having more than one “thing in the middle” is acceptable, things can get complex when you do that. See Bellemare and Bloem (2019) for more. The diagram then looks like Figure 9.7.

Figure 9.7: A Front-Door-Method Compatible Causal Diagram of Smoking

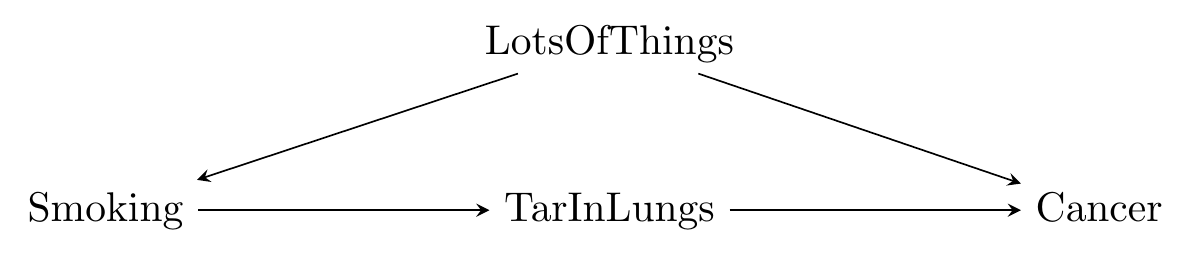
Given this diagram, let’s say that we look at the raw, unadjusted relationship between Smoking and TarInLungs and find that an additional cigarette per day adds an additional 15 grams of tar to your lungs over 10 years.

Then, we look at the relationship between TarInLungs and Cancer while controlling for Smoking and find that an additional 15 grams of tar in your lungs increases the chances of getting cancer by 2% over your lifetime.

So, then an additional cigarette per day increases the tar in your lungs by 15 grams, which in turn increases your probability of cancer by 2%. So an additional cigarette per day increases your probability of cancer by 2%.

That’s the front door method! So why is it not used very often? Largely because it requires that there be some variable like M or TarInLungs in those diagrams that exists entirely between Treatment and Outcome without being linked to anything else, and capturing a large portion of the reason why Treatment affects Outcome. That’s a lot of conditions that need to be met before a method can be used. Worse, these conditions don’t seem to pop up in the real world all that often. But hey, again, maybe you can figure it out.