Chapter 7 - Drawing Causal Diagrams

7.1 Our Idea of the World
We have a basic idea now about how causal diagrams work. But that assumes we have a causal diagram to work with. How can we get one? We’ll have to draw one ourselves.
Causal diagrams represent the data generating process (DGP) that got us our data. Drawing our own causal diagram will come down to putting our idea of what the DGP is onto paper (or a computer screen).
This can be tricky! It requires that we know as much as possible about that DGP before getting started. So the first step in drawing a causal diagram is really to do some research. Lots and lots of research on your topic.
Once you’ve done that, you can combine what you’ve learned with your intuition, follow this chapter, and suddenly, hey, there it is - a causal diagram. One step closer to answering that research question.
7.2 Thinking Through the Data Generating Process
How can we possibly write the world down in a graph? After all, the world is very complex, and a graph is clean and simple. But we’ll figure it out.
The key is to focus in as much as possible. Think about our research question and try to live in the world of that research question. We can’t possibly put everything in the world on our graph, so we need to work hard to not fall for the trap of trying to do so. What we can do is try to put everything relevant to our research question on the graph.
All through the process, we’re going to want to keep in mind that we’re trying to make a graph that mimics the data generating process (DGP) relevant to our research question. What leads us to observe the data we do? What causes the outcome? What causes the treatment?
It will probably help if we work with an example.
Let’s walk through a study that I worked on. That way, I can tell you exactly what sorts of things we were thinking about when considering what we thought the DGP looked like. In this study, we were interested in the effect of taking online courses on staying in college, specifically in community college in Washington State.
Our first task will be thinking through the list of relevant variables.
First off, just so we’re clear, what is a variable? We’ve covered this in previous chapters, but it bears repeating since it’s easy to forget when applying this stuff to the real world.
A variable on a causal diagram is a measurement we could take that could result in different values. So, for example, one of the variables relevant to our research question is “online class.” Is the class you’re taking online? - That’s the measurement. It could be “yes,” it could be “no” - those are the values. If we like, we could call it “type of class” with the values “online class” and “face-to-face class.” Notice that we don’t have one variable for “online class” and another for “face-to-face class.” That’s because those aren’t two separate variables, they’re two separate values that the same variable could take.
Treatment variable. The variable we want to know the effect of. How does it affect the outcome?
Outcome variable. The variable we want to know the effect on. How does the treatment variable affect it?
So there’s one relevant variable - online class. That’s our treatment variable. We’re interested in the effect of that variable. Another relevant variable will be “dropout” - did the student drop out of college since taking the class? This is our outcome variable. Treatment and outcome are always a good place to start.
Variable list:
- OnlineClass
- Dropout
All right, now what else?
We want to include all variables relevant to the DGP. That means any variable that has something to say about whether we observe online class-taking, or whether we observe dropout, or whether we observe them both together or apart. Every variable that causes the treatment or outcome, or causes something that causes something that causes the treatment or outcome, or causes something that causes something that causes something… is a good candidate for inclusion.
What are some things that might cause people to take online classes? Well, different students have different preferences for or against online courses, so Preferences. Those preferences might be driven by background factors like Race, Gender, Age, and SocioeconomicStatus. Those same background factors might influence how much AvailableTime students have - time-pressed students may prefer online courses. And AvailableTime might be influenced by how many WorkHours the student is doing. You also need solid InternetAccess to take online courses.
Now how about things that might cause people to drop out of community college? Some of the same background factors as before might be relevant, like Race, Gender, socioeconomic status (SES), and WorkHours. Your previous performance in school, Academics, is also likely to be a factor.
Now what does our list look like?
- OnlineClass
- Dropout
- Preferences
- Race
- Gender
- Age
- SES
- AvailableTime
- WorkHours
- InternetAccess
- Academics
This is a good time to pause, look at our list, and think hard about whether there’s anything important that we’ve left off. You may be able to think of a thing or two. But for now, let’s leave it at that.
How can we tell if something is important enough to be included? I just mentioned we should think about whether there’s anything important being left off. But how can we tell if a variable is important or not?
What it really comes down to is how strong we think the causal links out of that variable are.
For example, the presence of QuietCafes in someone’s area might encourage them to take an online course. A nice quiet place outside the house to do schoolwork. That may well be a real thing that encourages a few additional students to take online courses. But it’s unlikely to really be a determining factor for too many students.
So yes, it’s relevant, but it seems unlikely that it would have anything but a tiny effect, on average, on whether a student takes an online course. So we’re probably okay leaving it out.
With our set of variables in hand, we must try to think about which variables cause which others.
Conveniently, we’ve already done most of the work here. When we were thinking about which variables to include, we were asking ourselves what variables might be out there that cause our treatment or outcome variables. So we already have an idea of what might cause those.
What’s left is to think about how those variables might cause each other, or perhaps be caused by the treatment or outcome. We might also want to consider whether any of the variables are related but neither causes the other, in which case they must have some sort of common cause we can include.
We already have some causes of our treatment and outcome, as well as some other causes, from how we described the variables as we introduced them in the previous section:
- OnlineClass:117 This (especially in light of several demographic causes below) would be an excellent time to point out two things about this process: (1) There’s no sign implied here—none of these causal arrows say whether a given cause makes dropout more or less likely, just that it changes the distribution in some way, and (2) the mechanism might be omitted—having the arrow doesn’t say why one thing causes another, just that it does. In most cases you could drop another variable in the middle of the cause and caused variables, perhaps “School Spirit” or “Education Quality” in this case if you like, to explain the link. But often we don’t have enough information to quantitatively study every mechanism, so we leave it out for a later study, or theorize outside the diagram about what we think the mechanism might be. causes Dropout
- Dropout
- Preferences: causes OnlineClass
- Race: causes Dropout
- Gender: causes Dropout
- Age: causes Dropout
- SES: causes Dropout
- AvailableTime: causes OnlineClass, Dropout
- WorkHours
- InternetAccess: causes OnlineClass
- Academics: causes Dropout
How about which non-treatment and non-control variables cause each other? Age certainly causes SES, and all of the background variables (Race, Gender, Age, SES) affect AvailableTime and WorkHours. SES probably causes InternetAccess as well.
How about which variables are related to each other without there necessarily being a clear causal arrow in either direction? In this case, we add on common causes we can just call U1, U2, etc., that cause both variables. Our diagram isn’t really omplete if two variables on the diagram have a common cause but we’ve left that common cause off. Even if we can’t pin down what exactly that common cause is, it should be on there as an unknown.
Academics and SES are clearly correlated with Race and Gender, so we’ll want to have some sort of common cause there. Academics might also be related to the kinds of employment someone has and so affect WorkHours. InternetAccess is also likely to be caused not just by SES, but also Location, which we’ve left out up to now. So Location might want to get in that list.
Now what do we have?
- OnlineClass: causes dropout
- Dropout
- Preferences: causes OnlineClass
- Race: causes Preferences, Dropout, AvailableTime, WorkHours, related to Academics, SES
- Gender: causes Preferences, Dropout, AvailableTime, WorkHours, related to Academics, SES
- Age: causes Preferences, Dropout, SES, AvailableTime, WorkHours
- SES: causes Preferences, Dropout, InternetAccess, AvailableTime, WorkHours
- AvailableTime: causes OnlineClass, Dropout
- WorkHours: causes AvailableTime
- InternetAccess: causes OnlineClass
- Academics: causes Dropout, WorkHours, related to Race, Gender
- Location: causes InternetAccess, related to SES
And now that we have our list, we can draw a diagram. With a list this long and this many causal arrows described, I can warn you it’s going to be a little messy. Okay, very messy. That can happen. We’ll be coming back to clean it up a bit later.
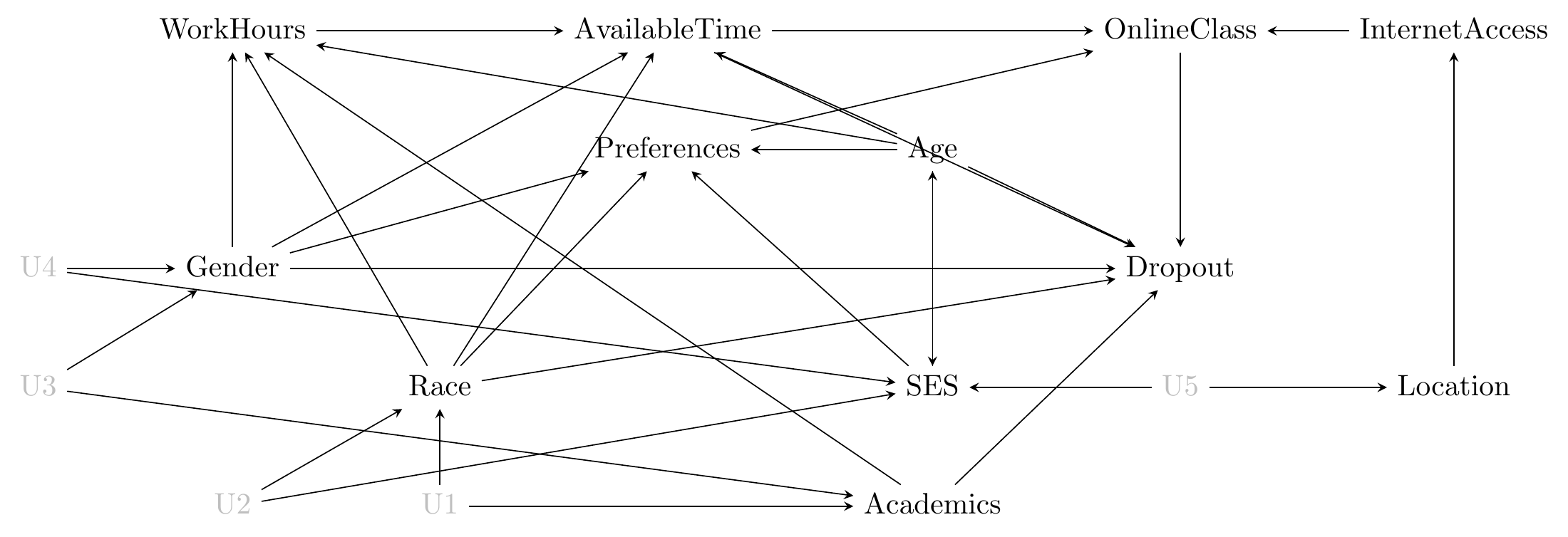
Figure 7.1: A Messy Diagram of the Effect of Online Classes on Dropout
And there we have our diagram in Figure 7.1. Now that we do, it’s a good time for revision. Looking at the diagram, what might be left off? What variables are likely to be relevant but aren’t there? What arrows should probably be there but aren’t?
There are probably a lot of things we’re missing here. A big one is the specific community college being attended - some offer lots of online courses and some don’t! So that’s likely to be a big cause of OnlineClass, and caused by plenty of other things on the list, especially Location.
But that’s not all. It’s a good exercise to look at a causal diagram and think carefully about what’s both important and missing.
7.3 Simplify
The real world is complex. The true data generating process (DGP) is too.
That leads us to a problem. The whole point of having a model like a causal diagram is to help us make sense of the DGP and, eventually, figure out how we can use it to identify the answer to our research question.
But if the diagram we end up with looks like what we have in the previous section, we’re going to be very hard-pressed to make any sort of sense of it. It would be handy if we could simplify it in some way.
Why is it important to simplify? Ultimately, the more complex a causal diagram is, the less helpful it is likely to be. Imagine you were asking someone for directions to the next gas station and instead of saying “it’s two exits north on the freeway, then next to the Wendy’s,” they handed you a giant atlas where each page is so intricately detailed that it only covers a single square mile. Sometimes less information is more information.
The trick will be to simplify where we can without getting so simple that our diagram no longer represents the true DGP. It’s a bit too far in the other direction to take the atlas away and just say the nearest gas station is “on Earth somewhere.”
How can we hit that golden mean of simple but not too simple? We can apply a few simple tests to see if there’s any needless complexity in our diagram.
- Unimportance. We’ve already discussed this one - if the arrows coming in and out of a variable are likely to be tiny and unimportant effects, we can probably remove the variable.
- Redundancy. If there are any variables on the diagram that occupy the same space - that is, they have the arrows coming in and going out of them from/to the same variables - we can probably combine them and describe them together (this works even if there are arrows between some of the variables being grouped together).
- Mediators. If one variable is only on the graph as a way for one variable to affect another (i.e., B in A \(\rightarrow\) B \(\rightarrow\) C where nothing else connects to B), then we can probably remove it and just have A \(\rightarrow\) C directly.118 This is what I mentioned in an earlier footnote about the mechanism - why one variable causes another - being omitted.
- Irrelevance. This one will take some additional knowledge about causal paths from Chapter 8. Some variables are an important part of the DGP but irrelevant to the research question at hand. If a variable isn’t on any path between the treatment and outcome variables, we can probably remove the variable.
Can we apply these steps to our diagram in Figure 7.1? We’ve already done Unimportance and left a few variables off for that reason. Let’s leave Irrelevance for now since we haven’t gotten to Chapter 8 yet. Can we do Redundancy or Mediators?
We do have some variables that occupy the same space on the diagram and so might be redundant. In particular, Gender and Race have the exact same set of arrows coming in and going out. So we can combine those into one, which we can call Demographics.
How about Mediators? We have a few here, the most prominent of which is Preferences. Instead of having Gender, Race, SES, and Age affect Preferences and then have Preferences affect OnlineClass, we can just have those four variables affect OnlineClass directly. Another one here is Location \(\rightarrow\) Internet Access \(\rightarrow\) OnlineClass. We can chuck InternetAccess right out and lose nothing!
The last one is a bit less certain. WorkHours affects OnlineClass through AvailableTime. WorkHours and AvailableTime don’t quite fall under Redundancy, since Academics affects WorkHours but not AvailableTime. And they don’t quite fall under Mediators, because other variables besides WorkHours affect AvailableTime.
However, the other variables besides WorkHours that cause AvailableTime also cause WorkHours. So if we got rid of AvailableTime and just had WorkHours affect OnlineClass directly (Mediators), we’d still have all those same AvailableTime causes affecting WorkHours and wouldn’t lose anything (Redundancy). The only sticky thing is that Academics doesn’t cause AvailableTime. But that’s fine in this case, because Academics does cause AvailableTime… through WorkHours! We do lose a little bit of information with this simplification because of the Academics variable, so we’d have to think carefully about whether we’re okay with that.
Now we have the much-better-looking, although still slightly messy, causal diagram below:
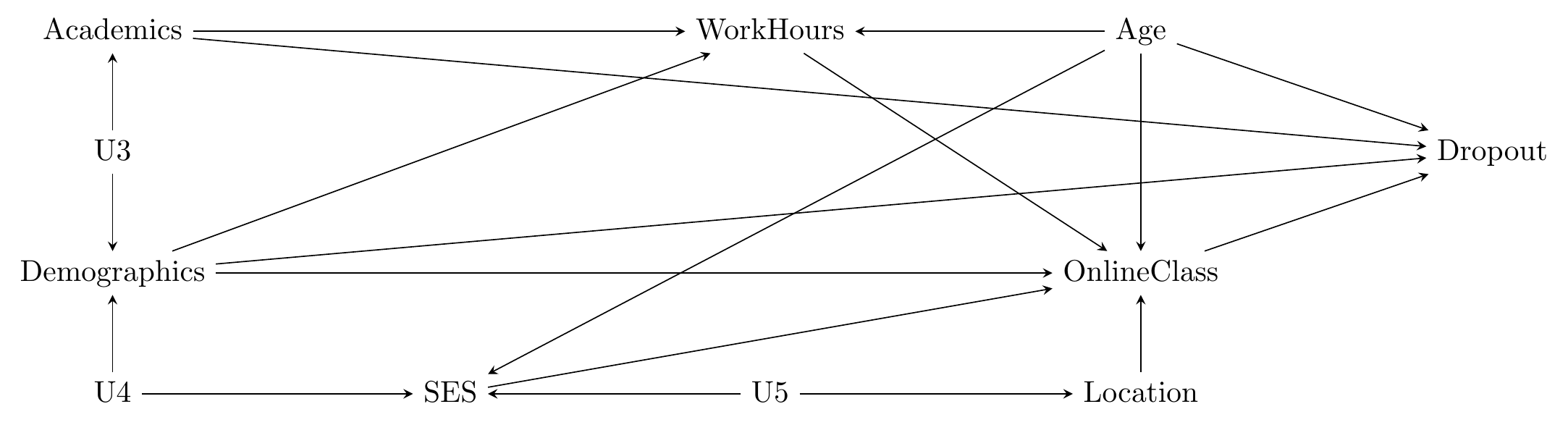
Figure 7.2: A Cleaner Diagram of the Effect of Online Classes on Dropout
While these steps can come in very handy, pay close attention to the use of “probably” in each of them. We can’t just apply these blindly. Even if a variable is subject to one of these steps, we don’t want to remove it if it’s key for our research design or crucial for communicating what’s going on.
For example, let’s say we’re interested in the effect of exercise on your lifespan. One reason exercise might lengthen your lifespan is because it raises your heart rate, and another reason is that it develops muscle. Heart rate and muscle development might be subject to the Mediator step - if the only arrows pointing to them are from exercise, and the only ones out are to lifespan, then we could eliminate both and just have exercise point to lifespan. But if we’re interested in why exercise works (is it heart rate or is it muscle?), we’d have no hope of answering that question if heart rate and muscle development aren’t actually on the diagram. So that would be a simplification too far.
To give another example, just a few paragraphs ago we eliminated InternetAccess because it was a mediator. But in the original study we’re talking about, the fact that InternetAccess caused OnlineClass was crucial because it acted as an “instrument” (Chapter 19). If we did that simplification in our study, there would be no study!
7.4 Avoiding Cycles
There is one thing a causal diagram cannot abide, and that is cycles. That is, you shouldn’t be able to start at one variable, follow down the path of the arrows, and end up back where you started.
There are two examples of graphs with cycles below in Figure 7.3. In the first one, you can go A \(\rightarrow\) B \(\rightarrow\) C \(\rightarrow\) A. In the second, the variables cause each other, and so you can just go A \(\rightarrow\) B \(\rightarrow\) A.
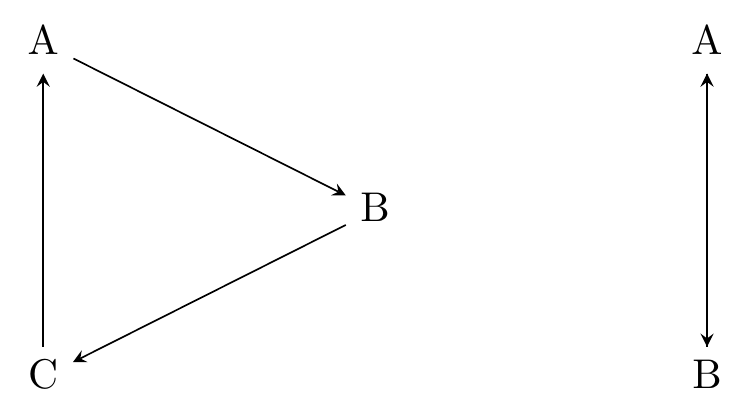
Figure 7.3: Two Causal Diagrams with Cycles
Why can’t we have this? Because if we do, then a variable can cause itself, and suddenly we’ve lost all hope of ever isolating the cause of anything, since we can’t separate the effect of B on A from the effect of A on B on A from the effect of B on A on B on A… and so on.
But hold on a minute. Surely there are plenty of real-world data generating processes (DGPs) with feedback loops like that. The rich get richer, objects have momentum, and if I punch you that makes you punch me, which makes me punch you.
Surely we’re not just going to have to give up any time this happens?
Well, no. But that’s because in the true DGP there can’t really be any cycles, if you think about it right. That’s because of time.
Let’s think about that punching feedback loop. It certainly seems like the diagram should look like Figure 7.4.
Figure 7.4: A Diagram About Punching

But that’s not quite right. After all, if I punch you, and you punch me back, that doesn’t cause me to send the first punch - it can’t, I already did it. It might, however, cause me to punch again later.
Let’s pay attention to when these punches are thrown. As is common in statistical applications where time is a factor, let’s refer to these time periods as \(t\), \(t+1\), \(t+2\), and so on, where \(t\) is “some particular time,” \(t+1\) is “the time right after that,” and so on. Now the diagram looks like Figure 7.5, and the cycle is gone. The diagram as is only has \(t\) and \(t+1\), but we could keep going out to the right with \(t+2\), \(t+3\), and so on, if we wanted.
Figure 7.5: Cycles are Even Worse than Punching. But Also Don’t Punch People.
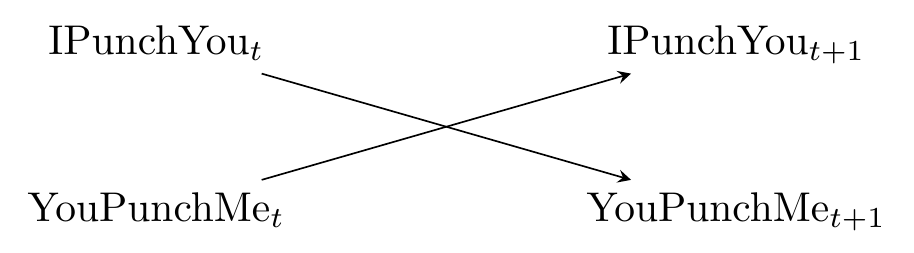
Whenever we have a cycle in our diagram, we can get out of it by thinking about adding a time dimension. And it has to work - the cycles pop up because the arrows loop back on themselves. But time’s arrow only moves in one direction.
There’s another way to break a cycle in a causal diagram.119 This is a common approach when researchers think they have a cycle on their hands. Although for the reasons given in this section, maybe they shouldn’t actually think of it as a cycle on the true diagram. But even with the approach of breaking the cycle up by introducing time, there are still some very cycle-like elements there to work through in identification. If you can find a source of random variation for one of the variables in the cycle (say, with a randomized experiment), then if we just focus on the part of the variable driven by randomness, the effect can’t loop back on itself. So if instead of waiting for you to punch me, I decide to punch you based on the outcome of a coin flip, then we still have \(IPunchYou \rightarrow YouPunchMe\) in the diagram, but instead of \(YouPunchMe \rightarrow IPunchYou\) we have \(CoinFlip \rightarrow IPunchYou\). Now the cycle is broken.120 This approach still leaves you with some problems if you can’t randomly determine all of the variable. See, for example, the discussion of social networks in Chapter 23.
7.5 Getting Comfortable with Assumptions
In this chapter, I’ve emphasized that your causal diagram should be based as much as possible on real-world knowledge and prior research. But since we can’t possibly know everything about every part of the data generating process (DGP), it also contains a lot of assumptions.
That’s both necessary and scary! Writing down a diagram like this means sticking your neck out. This causes that, you have to say. That doesn’t cause this, or at least not enough to draw an arrow. This other thing isn’t even worth including on the diagram. You think surely this will draw the pitchforks outside your door, or at least a slight disapproving glance from a professor.
But in order to progress, the assumptions do have to be made. The quality of your research will hinge on how accurate those assumptions are. So how can we get comfortable with the idea that we have to make assumptions, and how can we make those assumptions as accurate as possible?
The convenient thing about empirical work is that assumptions are rarely right or wrong. They’re more on a scale of probably-false to probably-true.
After all, if we have to make an assumption, it’s usually because there’s a gap in our knowledge. There’s no way to know for sure. Unlike a math problem, it’s not up to us to prove we’re right, but rather to get a critical reader to think “okay, that sounds plausible. I buy it.”
So it’s not our job to prove we’re right, at least not in the mathematical sense of “prove,” but it is our job to get that critical reader to buy it.
That narrows down our work for us. For a given assumption, ask yourself: “Is this probably true? What evidence can I provide to push this away from possible and toward probable?”
Put yourself in the head of that critical reader. Why might they not believe that assumption? What evidence could they be shown to convince them? Then, produce whatever evidence you can.
For example, let’s say you’re drawing a diagram of whether door-knocking for a candidate actually increases votes for that candidate. On your diagram there’s no arrow between “how much money the candidate has” and “having a door-knocking campaign.”
A reader might think “hold on… surely candidates with more money can more easily afford a door-knocking campaign, right? There should be an arrow there.” And to that you would look at whatever evidence you had. Do you have prior studies about the effects of candidate campaign coffers? Check them! Do you have data on the topic? Look in your data to see if there’s a correlation between money and door-knocking. Neither of these things would truly prove that the arrow shouldn’t be there, but they might help tip that reader’s scales from skeptical to buying-it (and gives you an opportunity to find out that your assumption was, in fact, wrong, so you can fix it).
That’s a lot of what it comes down to. Think about whether our assumptions are reasonable, try to base them as much on well-established knowledge and prior research as possible, and if we think there’s reason to be skeptical of them, ask what evidence would support the assumption and try to provide that evidence.
There are a few other approaches we can take that can help.
The first is just to get another set of eyes on it. It can be hard to be skeptical of your own assumptions - you made them, after all, so you probably think they’re pretty reasonable. But maybe there are reasons to be skeptical that you didn’t think of! Show your model to another person, especially a person who knows something about the setting or topic you’re trying to make a causal diagram for. Or just describe some of the assumptions you made and see what they think. You might be surprised with what they are and are not okay with.
There are also some more formal tests you can do. One nice thing about causal diagrams is that they produce testable implications for us. That is, once we have the diagram written down, it will tell us some relationships that should be zero. And we can check those relationships in our actual data using basic correlations. If they’re not zero, something about our diagram is wrong! We’ll talk more about these formal tests in Chapter 8.
Page built: 2025-10-17 using R version 4.5.0 (2025-04-11 ucrt)